Funciones logarítmicas
Reciben el nombre de funciones logarítmicas aquellas de la forma:
|
FUNCIÓN LOGARÍTMICA y = loga x , (a > 0) |
La definición de logarítmo, , que el lector ya conoce , muestra cómo la función logarítmica es la inversa de la exponencial. Es esta característica la que define los logaritmos.
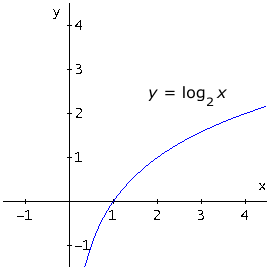 |
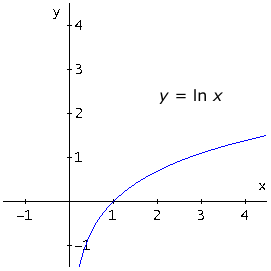 ln x = loge x |
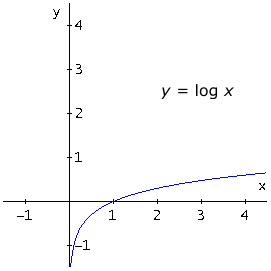 log x = log 10 x |
En los ejemplos expuestos la base (2, e, 10) es mayor que uno (a > 1) . 
Cuando la base es menor que uno (0 < a < 1) el logaritmo es decreciente. 
|
Las gráficas se pueden obtener mediante tablas XY pero, dado que la función logarítmica es inversa de la exponencial, es más cómodo recordar la relación entre las gráficas de f (x) y f −1(x) . Estas eran simétricas entre sí respecto de la bisectriz del primer y tercer cuadrantes y se puede obtener una a partir de la otra sin más que efectuar un giro de 180º en torno a esa bisectriz. Esta propiedad se muestra en la escena de la izquierda. |
Algunas características:
-
Las funciones logarítmicas tienen por dominio (0, +∞). Son siempre continuas.
-
Si la base es mayor que uno (a > 1) la función es creciente. Crece de manera muy lenta para x > 1.
-
Si la base es menor que uno (0 < a < 1) la función es decreciente.
-
Pasan por el punto (1, 0), que es su única raíz; no cortan al eje Y.
-
El eje Y es asíntota vertical. Para a > 1 esto se expresa en la forma:
(Un estudio más detallado de las "ramas infinitas", como es el caso de estas ramas asíntóticas, se aborda más adelante, en esta unidad)